Como vimos anteriormente, es necesario convertir nuestros tokens en números para que puedan ser procesados adecuadamente por una computadora y en consecuencia por nuestro modelo. Pero, ¿Es solo por eso? ¿O hay alguna otra razón por la que es conveniente trabajar con números?
Vimos que, para generar el siguiente token, era necesario conocer la relación entre los tokens de la frase de entrada (\(x\)), así como el conocimiento adquirido (\(w\)). Sin embargo, para una computadora, un token o palabra por sí sola no tiene significado, al menos no como lo tiene para nosotros, por lo que en principio no puede compararlas ni establecer relaciones semánticas entre ellas.
En cambio con los números sí podemos establecer algunas relaciones, tales como: determinar si un valor es mayor que otro, si es el doble de otro, podemos sumarlos o multiplicarlos. Es decir, si logramos representar adecuadamente los tokens con números, podríamos establecer sus relaciones de manera indirecta a través de valores numéricos. Veamos un ejemplo.
Supongamos que los ingresos mensuales de Jorge son 1,000 dólares. Hasta aquí, este dato individual no nos dice mucho. Sin embargo, si añadimos que Valeria gana 3,000 dólares, podemos establecer que ella gana el triple de Jorge, lo que nos proporciona más información de Jorge respecto a Valeria y viceversa.
Si, además, mencionamos que Alicia gana 4,000 dólares, ahora tenemos más relaciones entre los tres nombres). Incluso podemos expresar lo siguiente en términos de ingresos mensuales:
Alicia - Valeria = Jorge
Como vemos, por si mismos los nombres de las personas del ejemplo no tienen un significado para la computadora más allá del texto como tal, pero a través de representar características de estos con valores numéricos, pero sobretodo de las relaciones entre estos valores, es que la computadora puede indirectamente definir una categoría para cada token o palabra.
Nuevamente las relaciones aparecen como elemento fundamental.
Desde nuestro punto de vista humano, estas categorías podrían corresponder a categorías gramaticales, como sustantivos, adjetivos o verbos. Sin embargo, esta representación interna y categorización no necesariamente tiene que ser un concepto que reconozcamos o tenga sentido para nosotros, el modelo encontrará la manera más útil de hacerlo con el objetivo de predecir o generar el siguiente token.
Palabras y características: De tokens a embeddings
Un token puede tener múltiples características que la describan a través de valores numéricos, y estas características pueden estar interrelacionadas con las de otros tokens.
Volvamos a nuestra lista de tokens iniciales.
azul → 227
cielo → 350
frio → 402
el → 578
es → 698
En lugar de un único valor, asignemos a cada token dos números, de tal manera que nos permite representar dos características.
azul → [-0.2, 0.9]
cielo → [0.8, -0.1]
frio → [-0.4, 0.7]
el → [0.3, -0.6]
es → [0.1, -0.1]
Esta lista de valores la denominaremos vector, si has llevado un curso de álgebra lineal seguro ya conoces la notación.
Estos valores también pueden ser aprendidos y/o optimizados por el modelo, así que por ahora asignémosles unos valores y más adelante veremos como se establecen con el entrenamiento del modelo.
¿Qué representa cada característica? En realidad, lo importante no es tanto el significado individual de cada una, sino cómo se relacionan y agrupan ciertos tokens. Sin embargo, para fines ilustrativos, imaginemos que la primera característica indica en qué medida un token es un sustantivo, y la segunda, qué tanto funciona como un adjetivo.
También podemos interpretar estos vectores como coordenadas y cada una de las posiciones una dimensión. Siempre que tengan tres dimensiones o menos, podemos representarlos gráficamente. Veamos como sería una gráfica con los valores de nuestro diccionario.
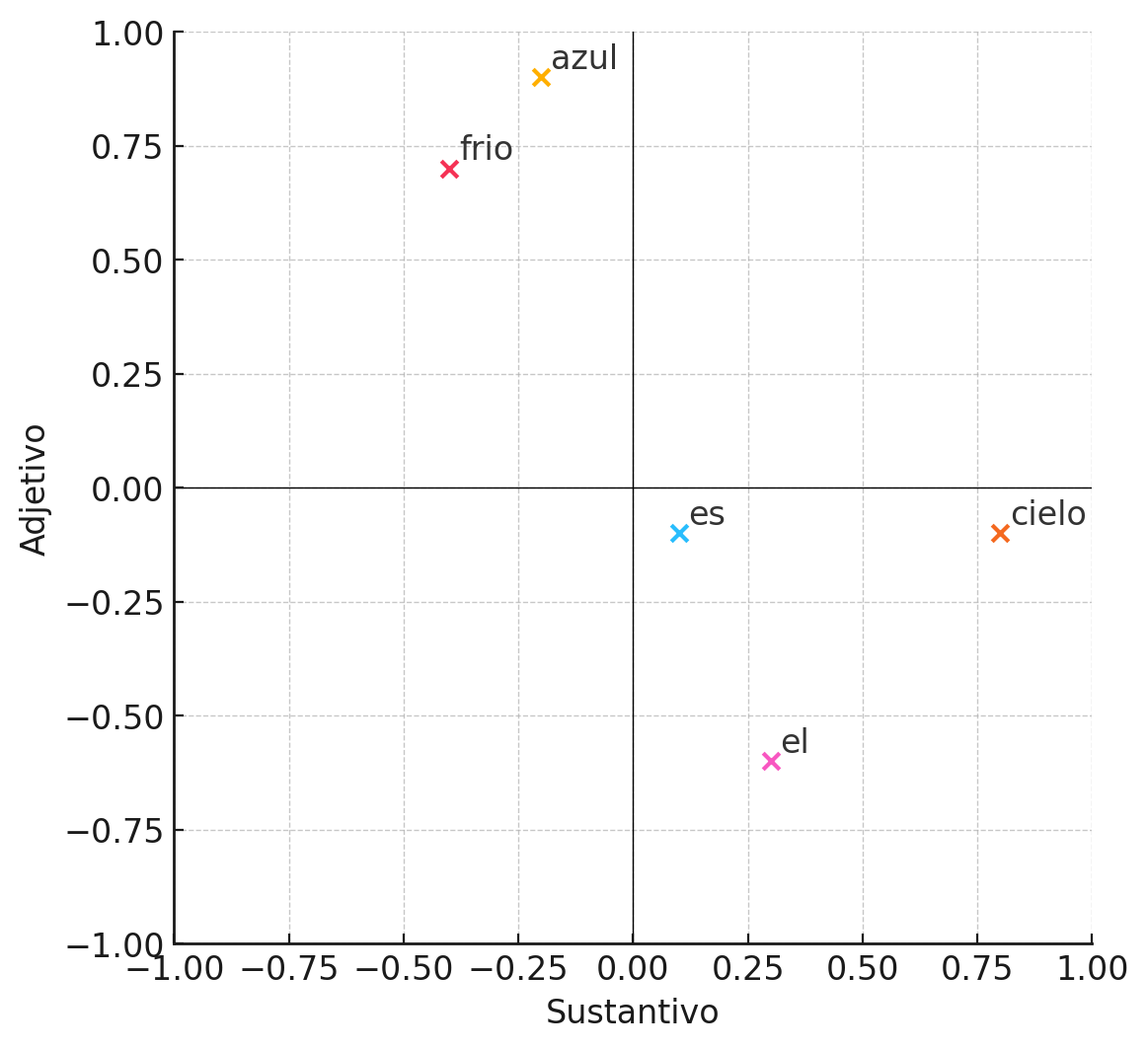
Representación de embeddings
Cada eje o dimensión del gráfico representa una característica. Podemos observar cómo los tokens se agrupan según su “cercanía” semántica en función de los valores de estas características. Con esto podemos deducir que los valores más adecuados serán los que mejor separen y junten ciertos valores o que representen mejor estas relaciones.
Finalmente, a estas representaciones vectoriales de los tokens los denominaremos embeddings. En modelos como GPT-3 el tamaño de los embeddings fue de 12288 valores.
Actualización de nuestro modelo
Usemos ahora este nuevo concepto dentro del modelo que hemos trabajado hasta ahora.
(Vamos a usar una notación similar a la de Python para simplificar la representación de las ideas y porque LaTeX no es muy bien soportado aquí)
Nuestra entrada \(x\) sería la siguiente, el cual seria una matriz de 3 filas y 2 columnas
x = [[0.3, -0.6],
[0.8, -0.1],
[0.1, -0.1]]
Pero dado que nuestro modelo es muy simple y solo soporta un único vector de entrada, vamos a combinar todos los valores de cada token en un solo vector.
x = [0.3, -0.6, 0.8, -0.1, 0.1, -0.1]
Ya que ahora tenemos seis valores, definimos un vector de igual tamaño para los pesos, para realizar la operación de nuestra función \(f_1\)
w_f1 = [1, 0.5, 1.5, 1, 0.5, 1.5]
Multiplicamos ambos vectores, la cual será valor por valor en cada posición \((x_1 \times w_1, x_2 \times w_2, \ldots)\), y sumamos el resultado
f1(x) = sum(x * w_f1)
= sum([0.3, -0.3, 1.2, -0.1, 0.05, -0.15])
= 1.0
Ahora ingresamos ese valor en la función \(f_2\)
w_f2 = [2.5, 0.7, 2.0, 0.2, 0.5]
f2(x) = x * w_f2
= 1.0 * w_f2
= [2.5, 0.7, 2.0, 0.2, 0.5]
Finalmente aplicaremos normalizaremos los valores, esta vez con softmax.
softmax(x) = [0.4982, 0.0823, 0.3021, 0.0499, 0.0675]
Si hacemos un muestreo de estos valores nuevamente obtendremos el mismo patrón del post anterior, en el que “azul” y “frío” son las elecciones más frecuentes.
Veamos un gráfico de todo el proceso de nuestro modelo para generar el siguiente token:
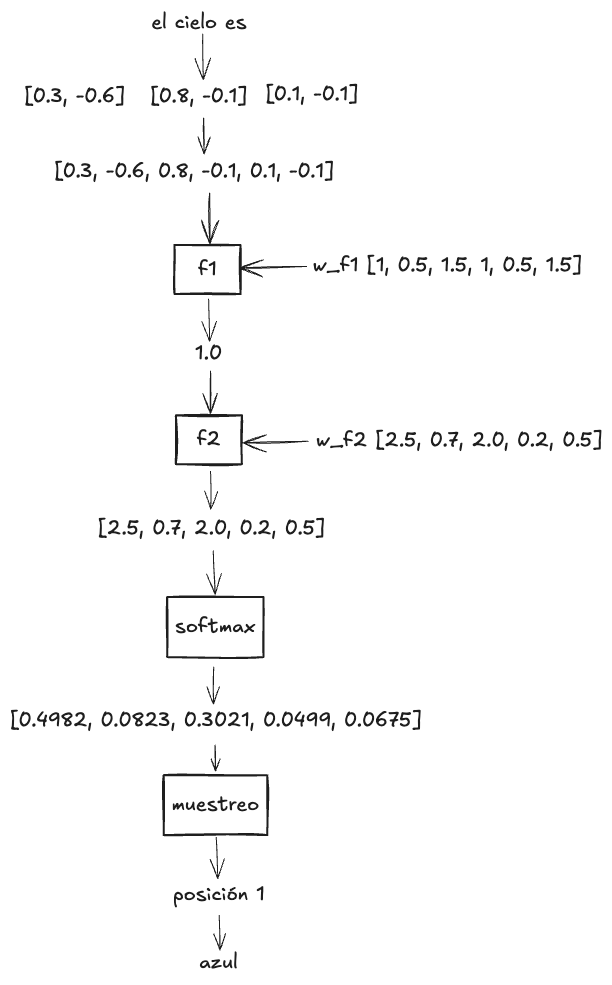
En conclusión, hemos explorado cómo representar los tokens mediante vectores, lo que nos permite definir sus características y asignarles valores numéricos, siendo estos esenciales para establecer relaciones entre los tokens.
Dejaré un ⮕ jupyter notebook donde podemos ver una implementación en Python de lo que hemos visto.
- Parte 1: Mi camino a entender (por fin) los LLMs: Relaciones y funciones
- Parte 2: Mi camino a entender (por fin) los LLMs: Creatividad y probabilidades
- Parte 3: Mi camino a entender (por fin) los LLMs: Vectores y embeddings