Anteriormente vimos como el concepto de función nos sirve para representar un modelo de lenguaje y sus principales componentes.
\[ y = f(x, w) \]Habíamos visto también que uno de los problemas de nuestro modelo era que nuestra predicción de la palabra siguiente no tenia mucha variabilidad o “creatividad”, es decir para la misma frase de entrada la palabra generada era siempre la misma. En este post abordaremos como solucionar este problema.
De aquí en adelante usaremos el termino token en lugar de palabra.
Recordemos los números que habíamos asignado a nuestros tokens.
azul → 227
cielo → 350
frío → 402
el → 578
es → 698
Por el momento, para fines didácticos, asumamos que estas son los únicos tokens que nuestro modelo conoce y puede procesar.
A este conjunto de tokens lo llamaremos nuestro “diccionario”. Por ejemplo se calcula que al diccionario para entrenar GPT-3 tenia 14735746 tokens.
Para darle variabilidad al resultado de nuestro modelo, en lugar de que este nos diga el siguiente token directamente, haremos que nos diga: cual es la probabilidad de que cada uno de los tokens de nuestro diccionario sea el siguiente token generado, de tal manera que la oración tenga coherencia.
Por ejemplo el resultado podría ser el siguiente
azul → 227 → 0.5
cielo → 350 → 0.05
frío → 402 → 0.3
el → 578 → 0.13
es → 698 → 0.02
Donde los tokens con mayor probabilidad serían “azul” 50% y “frio” 30%. Nótese que la suma de todas las probabilidades es 100%.
Anteriormente vimos nuestro modelo como una única función, pero en realidad estos modelos están compuestos por varias funciones, esto nos permite tener capas independientes que internamente el modelo optimiza para una tarea concreta, y para la cual asigna pesos independientes.
Teniendo en cuenta lo anterior, vamos dividir nuestra función \(f\), que representa a nuestro modelo global, en dos funciones internas, que llamaremos \(f_1\) y \(f_2\).
La primera, \(f_1\), es similar a la que ya habíamos visto:
\[ f_1(x_1, x_2, x_3) = x_1 w_1 + x_2 w_2 + x_3 w_3 \]\(x_1\), \(x_2\) y \(x_3\) son nuestra frase de entrada, en nuestro ejemplo era: “el cielo es”
La forma de esta función es arbitraria, es solo para fines ilustrativos, pero en modelos reales la elección forma parte de elegir la arquitectura del modelo.
y la segunda, \(f_2\), sería:
\[ f_2(x) = x \times w_1, x \times w_2, \ldots, x \times w_5 \]La entrada \(x\) de esta función \(f_2\) será la salida de la función \(f_1\). Esta función tiene la finalidad de dar un “puntaje” a cada uno de los tokens de nuestro diccionario, es por ello que la entrada de está función se multiplica por cada uno de 5 valores \(w\) para producir 5 valores de salida, ya que nuestro diccionario tiene 5 tokens. Este puntaje es la probabilidad de ser la palabra escogida como palabra siguiente.
En este punto, podemos notar que tenemos una composición de funciones, ya que la entrada de una función corresponde a la salida de otra.
\[ f_2(f_1(x_1, x_2, x_3)) \]Conectar operaciones a través de la composición de funciones nos será de mucha utilidad cuando hagamos el entrenamiento del modelo más adelante.
Vayamos a un ejemplo numérico
(Asumiendo que nuestro modelo ya tenga valores de \(w\) óptimos, en futuros posts veremos como determinarlos con el entrenamiento).
Asignemos los siguientes valores a \(w\) de \(f_1\)
\[ \begin{align*} w_1 &= 1.0 \\ w_2 &= 0.5 \\ w_3 &= 1.5 \end{align*} \]Y los siguientes valor a \(w\) de \(f_2\)
\[ \begin{align*} w_1 &= 2.5 \\ w_2 &= 0.7 \\ w_3 &= 2.0 \\ w_4 &= 0.2 \\ w_5 &= 0.5 \end{align*} \]Hagamos los cálculos
\[ \begin{align*} f_1(578, 350, 698) &= 578 \times 1.0 + 350 \times 0.5 + 698 \times 1.5 \\ &= 1800.0 \end{align*} \]\[ \begin{align*} f_2(1800) &= 1800 \times 2.5, 1800 \times 0.7, 1800 \times 2.0, 1800 \times 0.2, 1800 \times 0.5 \\ &= (4500, 1260, 3600, 360, 900) \end{align*} \]Luego de calcular el resultado de ambas funciones obtenemos un puntaje para cada uno de los tokens de nuestro diccionario, lo que nos indica cuales tokens son más esperados encontrar como token siguiente de nuestra frase.
azul → 4500
cielo → 1260
frío → 3600
el → 360
es → 900
Estos valores se denominan logits, los cuales podemos verlos como valores de probabilidad no normalizados.
Lo que haremos ahora será normalizar estos valores, lo haremos de una forma sencilla, dividiremos cada valor por la suma de todos los valores, como hicimos anteriormente definiremos una nueva función \(\text{norm}\) para esto.
\[ \text{norm}(x_1, x_2, \ldots, x_n) = \left(\frac{x_1}{\sum_{i=1}^{n} x_i}, \frac{x_2}{\sum_{i=1}^{n} x_i}, \ldots, \frac{x_n}{\sum_{i=1}^{n} x_i}\right) \]Esta notación puede parecer un poco complicada pero lo que hacemos simplemente es dividir cada valor por la suma de todos los valores que es 10620:
\[ \begin{align*} \text{norm}(4500, 1260, 3600, 360, 900) &= \frac{4500}{10620}, \frac{1260}{10620}, \frac{3600}{10620}, \frac{360}{10620}, \frac{900}{10620} \\ &= (0.42, 0.12, 0.34, 0.03, 0.09) \end{align*} \]Con esto tenemos una distribución de probabilidades, que nos da la probabilidad de cada palabra de nuestro diccionario de ser elegida como la siguiente palabra para la frase dada.
En modelos reales se suele usar una función llamada softmax para este propósito, la cual tiene la característica de producir una distribución de probabilidades donde los valores grandes se vuelven mucho más dominantes.
Notemos que con cada operación continuamos con la composición de funciones
\[ \text{norm}(f_2(f_1(x_1, x_2, x_3))) \]Finalmente, usaremos un método de muestreo sobre esta distribución de probabilidades para elegir la palabra siguiente, con esto las que tengan más probabilidad serán mas escogidas que las que menos probabilidad tienen.
Aquí podemos ver una representación gráfica de nuestro modelo conectando todas las funciones que hemos utilizado hasta ahora.
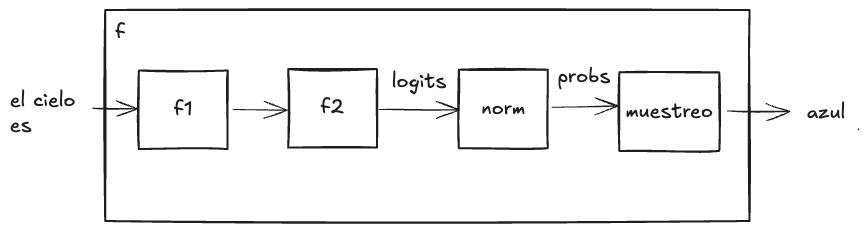
Representación gráfica de nuestro modelo.
Dejaré un ⮕ jupyter notebook donde podemos ver una implementación en Python de lo que hemos visto. Podemos ver por ejemplo como se generan (eligen) distintos tokens tras 10 ejecuciones para la misma frase de entrada según la distribución de probabilidad.
el cielo es azul
el cielo es frío
el cielo es cielo
el cielo es frío
el cielo es frío
el cielo es azul
el cielo es azul
el cielo es frío
el cielo es azul
el cielo es el
el cielo es azul
- Parte 1: Mi camino a entender (por fin) los LLMs: Relaciones y funciones
- Parte 2: Mi camino a entender (por fin) los LLMs: Creatividad y probabilidades
- Parte 3: Mi camino a entender (por fin) los LLMs: Vectores y embeddings